Trong toán học, chúng ta thường gặp các khái niệm về các tập hợp số khác nhau, như tập hợp số tự nhiên, số nguyên, số thực, số phức,… Mỗi tập hợp số có những đặc điểm và tính chất riêng biệt, phản ánh những khía cạnh khác nhau của thế giới số học.
Trong bài viết này, hãy cùng iamsale tìm hiểu về một tập hợp số rất quan trọng và phổ biến trong toán học, đó là tập hợp số hữu tỉ, hay còn được ký hiệu là Q. Tập Q là gì? Tại sao nó lại có ý nghĩa? Làm thế nào để biểu diễn và tính toán với các số hữu tỉ? Hãy cùng khám phá qua các nội dung sau đây:
1. Tập Q là gì?
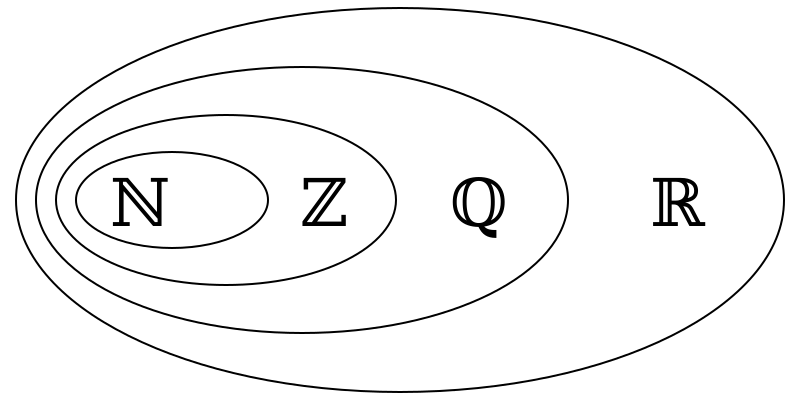
Tập Q là tập hợp các số hữu tỉ, được ký hiệu là Q. Số hữu tỉ là số có thể viết dưới dạng a/b với a, b ∈ Z và b khác 0. Ví dụ như 1/2, 3/4, 2/5 đều thuộc tập hợp Q. Tập hợp Q được sử dụng rộng rãi trong toán học và khoa học tự nhiên để đại diện cho các số có thể biểu diễn dưới dạng phân số.
Tập Q có nguồn gốc từ việc giải quyết các phương trình bậc hai trong toán học cổ điển. Khi ta muốn tìm nghiệm của phương trình ax^2 + bx + c = 0 với a, b, c ∈ Z và a khác 0, ta có công thức nghiệm như sau:
x = (-b ± √(b^2 – 4ac)) / 2a
Trong trường hợp b^2 – 4ac là một số chính phương (tức là có căn bậc hai là một số nguyên), ta có thể thu được các nghiệm x là các số nguyên hoặc các phân số có tử và mẫu là các số nguyên. Những số như vậy được gọi là số hữu tỉ. Ví dụ: Phương trình x^2 – 5x + 6 = 0 có hai nghiệm x = 2 và x = 3, đều là các số nguyên thuộc Q.
Tuy nhiên, không phải lúc nào b^2 – 4ac cũng là một số chính phương. Trong trường hợp này, ta sẽ thu được các nghiệm x có dạng a + b√c, trong đó a, b, c ∈ Z và c là một số không phải là số chính phương. Những số như vậy được gọi là số vô tỉ. Ví dụ: Phương trình x^2 – 2 = 0 có hai nghiệm x = ±√2, đều là các số vô tỉ không thuộc Q.
Như vậy, ta có thể thấy rằng tập Q là một tập hợp số rất tự nhiên và hợp lý, bởi vì nó bao gồm những số có thể giải được các phương trình bậc hai đơn giản nhất. Tập Q cũng là một tập hợp số rất cơ bản và quan trọng, bởi vì nó là một tập hợp đóng đối với các phép toán cộng, trừ, nhân, chia (trừ khi chia cho 0) và lũy thừa (với số mũ nguyên). Điều này có nghĩa là nếu ta thực hiện các phép toán này với các số hữu tỉ, ta sẽ thu được kết quả cũng là các số hữu tỉ.
2. Tại sao tập Q lại có ý nghĩa?

Tập Q có ý nghĩa vì nó là một tập hợp số rất phổ biến và thiết thực trong cuộc sống và khoa học. Các số hữu tỉ có thể biểu diễn cho nhiều khái niệm và đại lượng quan trọng, như tỉ lệ, phần trăm, phân số, xác suất, tỷ lệ, giá trị tuyệt đối,… Các số hữu tỉ cũng có thể được sử dụng để xấp xỉ các số vô tỉ hoặc các số thực khác bằng cách làm tròn hoặc cắt bớt các chữ số sau dấu phẩy. Ví dụ: Số π có giá trị xấp xỉ là 3.14 hoặc 22/7, đều là các số hữu tỉ.
Ngoài ra, tập Q cũng có ý nghĩa vì nó là một tập hợp số có cấu trúc đại số rất đẹp và đầy đủ. Tập Q là một trường (field), tức là một tập hợp số có hai phép toán cộng và nhân thỏa mãn các tính chất giao hoán, kết hợp, phân phối và tồn tại phần tử đơn vị và phần tử nghịch đảo.
Tập Q cũng là một không gian vectơ (vector space) trên chính nó, tức là một tập hợp số có hai phép toán cộng vectơ và nhân với một số thỏa mãn các tính chất giao hoán, kết hợp, phân phối và tồn tại vectơ không và vectơ đơn vị. Tập Q cũng là một miền tích (integral domain), tức là một tập hợp số có hai phép toán cộng và nhân thỏa mãn các tính chất giao hoán, kết hợp, phân phối và không có ước chung lớn nhất (gcd) khác 1.
3. Làm thế nào để biểu diễn và tính toán với các số hữu tỉ?

Có hai cách chính để biểu diễn các số hữu tỉ: dưới dạng phân số a/b hoặc dưới dạng số thập phân vô hạn tuần hoàn
- Dưới dạng phân số a/b: Đây là cách biểu diễn đơn giản và trực quan nhất của các số hữu tỉ. Ta chỉ cần viết số tử và số mẫu của phân số, với điều kiện số mẫu khác 0. Ví dụ: 1/2, -3/4, 5/1, 0/7 đều là các số hữu tỉ dưới dạng phân số. Để tính toán với các số hữu tỉ dưới dạng phân số, ta có thể sử dụng các quy tắc sau:
- Cộng hai phân số có cùng mẫu số: Ta chỉ cần cộng hai tử số lại và giữ nguyên mẫu số. Ví dụ: 1/4 + 3/4 = (1 + 3) / 4 = 4/4 = 1
- Cộng hai phân số có mẫu số khác nhau: Ta phải tìm bội chung nhỏ nhất (lcm) của hai mẫu số, rồi nhân hai phân số với các hệ số thích hợp để có cùng mẫu số, rồi cộng hai tử số lại. Ví dụ: 1/3 + 2/5 = (1 x 5 + 2 x 3) / (3 x 5) = (5 + 6) / 15 = 11/15
- Trừ hai phân số: Ta có thể sử dụng cách tương tự như cộng hai phân số, chỉ khác là trừ hai tử số thay vì cộng. Ví dụ: 2/3 – 1/6 = (2 x 6 – 1 x 3) / (3 x 6) = (12 – 3) / 18 = 9/18 = 1/2
- Nhân hai phân số: Ta chỉ cần nhân hai tử số và hai mẫu số lại với nhau. Ví dụ: 2/3 x 3/4 = (2 x 3) / (3 x 4) = 6/12 = 1/2
- Chia hai phân số: Ta có thể đảo ngược phân số thứ hai rồi nhân với phân số thứ nhất. Ví dụ: 2/3 : 3/4 = (2/3) x (4/3) = (2 x 4) / (3 x 3) = 8/9
- Dưới dạng số thập phân vô hạn tuần hoàn: Đây là cách biểu diễn khác của các số hữu tỉ, bằng cách chia tử cho mẫu và viết kết quả dưới dạng số thập phân. Tuy nhiên, do các số hữu tỉ có thể có nhiều chữ số sau dấu phẩy, ta không thể viết hết được tất cả các chữ số đó. Thay vào đó, ta sẽ nhận thấy rằng sau một lúc nào đó, các chữ số sẽ lặp lại một chu kỳ nào đó vô hạn lần. Khi đó, ta có thể viết các chữ số đó trong dấu ngoặc đơn để biểu thị sự lặp lại. Ví dụ:
- Số hữu tỉ 1/3 khi chia sẽ cho kết quả là 0.333… Tức là chữ số 3 lặp lại vô hạn lần sau dấu phẩy. Ta có thể viết tắt là 0.(3)
- Số hữu tỉ 22/7 khi chia sẽ cho kết quả là 3.142857142857… Tức là chu kỳ chữ số 142857 lặp lại vô hạn lần sau dấu phẩy. Ta có thể viết tắt là 3.(142857)
Trên đây là những thông tin giải đáp TẬP Q LÀ GÌ? . iamsale hi vọng bài viết này hữu ích với bạn!

